Ein bekanntes Problem, das mich jüngst in der Analysis wieder einholte, ist das Paradoxon, das Zenon von Elea bereits vor 2400 Jahren aufstellte und das bis in die jüngste Zeit viele Denker beschäftigte: Zenon behauptete, dass in einem Wettrennen zwischen dem sagenhaften Sprinter Achilles und einer Schildkröte der Held das Tier nie einholen würde, wenn sie einen Vorsprung bekäme.

[caption width="220" align="alignright"]{width=”220” height=”369”} Achilles denkt über Zenos Problem nach. (Quelle: Wikipedia)[/caption]
Er präsentierte damals folgende Überlegung: Wenn Achilles den Punkt erreicht, an dem die Schildkröte gestartet ist, ist diese bereits um ein Wegstück weiter. Erreicht er diesen Punkt, ist sie wieder weitergekrochen und so fort. Der Abstand würde sich verkleinern, aber einholen würde er sie nie. Natürlich widerspricht das jeder Erfahrung, denn in der Wirklichkeit würde der Sportler das Tier locker überholen.

Da dieses Paradoxon zum "Partywissen" gehört und immer wieder präsentiert wird, tut man gut daran, sich folgende Argumentation zu eigen zu machen. Außerdem zeigt es die unterschiedlichen Sichtweisen der antiken und der modernen Denkweisen ganz gut auf. Und nicht zuletzt kann man ein bisschen was über Analysis lernen.

Dem Achilles auf den Fersen

Nehmen wir einmal an, Achilles wäre viermal so schnell wie die Schildkröte; für unseren Helden also ein ganz lockerer Spaziergang. Dann wäre der Abstand a zu jedem Betrachtungszeitpunkt t genau

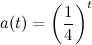{style=”border: none”}

Nun geht die antike griechische Philosophie nicht mit den Begriffen "Zeit" oder "Geschwindigkeit" um, die uns heutzutage so selbstverständlich erscheinen. Und tatsächlich berücksichtigt das Gedankenexperiment die Zeit nicht. Die Messungen im Gedankenexperiment finden nämlich zu den Zeiten

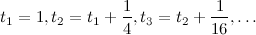{style=”border: none”}

usw. statt. Das bedeutet, dass nach der n-ten Messung gerade die Zeit

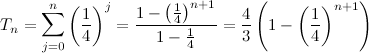{style=”border: none”}

vergangen ist, wie man sich mit der geometrischen Summenformel klar macht. Das bedeutet, dass keine der Messungen später als 4/3 der Anfangszeit stattfindet. Also holt Achilles die Schildkröte einfach nur nicht innerhalb der ersten 4/3 Minuten ein. Wie man zeigen kann, ist das auch einfach der Zeitpunkt, an dem die beiden gleichauf sind.

Wer Spaß an einer schrittweisen Erklärung der Betrachtung hat und sich nebenbei anschaulich das Quotientenkriterium erklären lassen möchte, schaut sich das Video von Numberphile (auf Englisch) an.